MepBay

Desenvolvida por Hsu & Evans (1989) através de uma séria de experimentos em escala reduzida, a equação baseia-se em uma relação entre características geométricas da praia e o ângulo de incidência das ondas predominantes. Para a aplicação da equação extrai-se por meio de uma imagem de satélite, foto aérea ou mapa os parâmetros listados a seguir para a resolução da Equação 01.

 

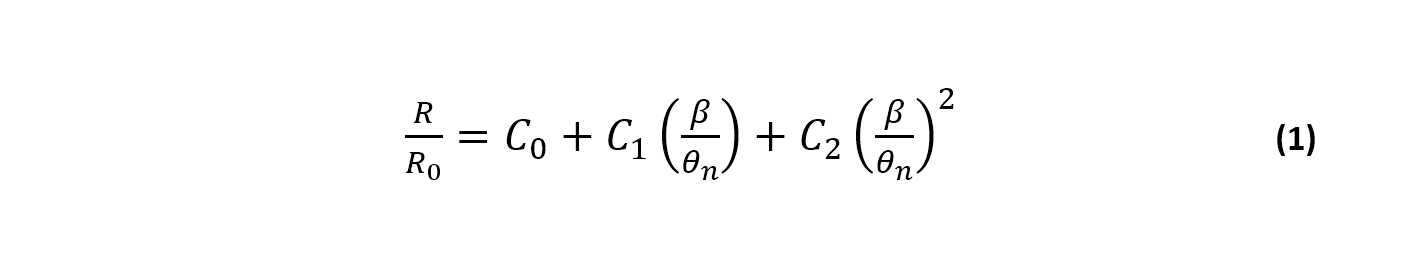
Parâmetros:

R₀ ou R_β (linha de controle ou raio inicial): linha que une o ponto de difração de ondas até a extremidade final da parte retilínea da praia;

Linha de cristas das ondas predominantes: a extração da obliquidade das ondas predominantes nas praias de enseada em questão é obtida através de imagens aéreas ou mapas utilizados, corresponde a uma linha paralela à parte retilínea da praia, a qual é transferida do ponto de difração;

R: Raios traçados a partir do promontório (ponto de difração), unidos ao longo da praia. Extraído a partir do ângulo θ e a linha de cristas das ondas predominantes;

β (ângulo beta): ângulo formado entre as linhas de crista de onda predominantes e a linha de controle R₀;

θ (ângulo teta): ângulo formado entre a linha de crista de onda predominantes e os demais raios R;

C₀, C₁ e C₂: obtidos em função do ângulo beta e definidos através de testes e experimentos tabelados (Hsu & Evans, 1989).

Para tal usa-se o sistema de coordenadas polares e devido as razões a equação é adimensional.

 

• Aplicação da equação de forma manual:

Para a aplicação do modelo parabólico utilizando um mapa, cartas topográficas, fotografia aérea vertical ou imagem de satélite de uma praia, devem-se seguir, de forma geral, os seguintes passos elencados a seguir. Destaca-se que a aplicação a equação é adimensional, não importando a escala dos mapas ou cartas topográficas.

De posse deste material procede-se da seguinte maneira:

1. Determinar o ponto de difração das ondas e o ponto final da praia;
2. Traçar R₀ (linha de controle), traça-se uma reta do ponto onde ocorre a difração de ondas até o ponto final da praia e efetua-se a medida do comprimento desta reta, como resultado se tem o R₀;
3. Traçara uma reta sobre a parte mais retilínea da praia e unir esta reta ao ponto de difração com régua paralela ou jogo de esquadros, sendo o ângulo formado entre estas denominado de ângulo beta, medido em graus, ou traçar a linha das cristas das ondas predominantes e transferi-la (paralelamente) até o ponto que esta linha cruza a linha de controle;
4. Para os raios R_, de posse de um transferidor, traçar linhas de 10 em 10 graus (até 150 graus) partindo do ponto de difração das ondas aos outros pontos da periferia da praia em questão enquanto houver areia. Assim, são obtidos os raios R para cada ângulo teta formado.
5. O comprimento dos raios R são determinar aplicada a Equação 01, sendo C₀, C₁ e C₂ obtidos em relação ao ângulo beta, seus valores são tabelados.
6. Após calculados todos comprimentos dos raios R, une-se as extremidades destes raios e se obtém a linha de costa teórica para praias em questão.

 

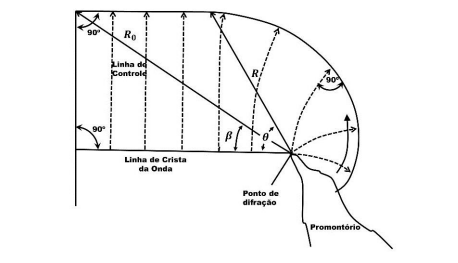Figura: Esboço de uma praia de enseada segundo abordagem parabólica. Fonte: Silvester & Hsu 1993, modificado. 

 

• Aplicando a equação assume-se que:

1. Célula fechada, não há entrada nem saída de sedimentos;
2. O segmento retilíneo da praia (setor mais exposto a ação das ondas) é normal a ortogonal das ondulações predominantes;
3. A batimetria entre as duas extremidades da praia é uniforme;
4. Ondas quebram simultaneamente ao longo da praia;
5. Transporte liquido de sedimentos ao longo da costa é zero em escala histórica.

 

• Considerações: 

Com a aplicação a equação e conhecimentos básicos, o usuário pode identificar se a praia se encontra em situação de equilíbrio estático, onde não ocorrem modificações morfológicas, ou equilíbrio dinâmico, quando ocorre modificações morfológicas. Sabe-se também, que a aplicação desta equação demanda de tempo e com o intuído de facilitar e agilizar esta resolução, o aplicativo MepBay foi desenvolvido para possibilitar ao usuário uma rápida solução do modelo parabólico, viabilizando o teste de diversas condições de praias entre situações existentes e teóricas.

 

REFERÊNCIAS: 

• Hsu, J. R-C., Evans, C. Parabolic Bay Shapes and Applications. In: Institution of Civil Engineers – Part 2, 1989, Londres. Proceedings… Londres: Thomas Telford, p.557-570, 1989.
• Silvester, R., Hsu, J.R.C. Coastal Stabilization: Innovative Concepts. Prentice-Hall, Englewood Cliffs, NJ. 578 pp. 1993