MepBay

Bay beaches or headland bay beaches, can be defined as a sandy shoreline bordered by rocky outcrops or promontories, whether natural or anthropogenic, where it assumes a curved shape (Klein, 2004). These beaches tend to develop an asymmetric form, characterized by a shadowed area near the rocky promontory, sheltered from wave energy, marked by a strongly curved region, a central region with gentle curvature, and the other end with more linear characteristics (Figure 01), typically parallel to the predominant direction of incident wave trains (Silvester & Hsu, 1997).

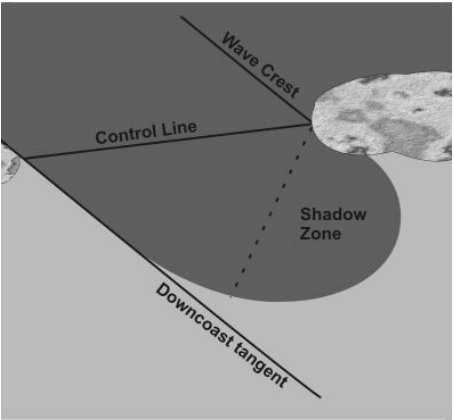
Figure 1: Principal components of a headland bay beach.

On a bay beach, the oblique incidence and wave height gradient along the coast promote the longitudinal transport of sediment, influencing the planform shape of the beach, transversely shaping itself to the predominant wave attack direction (Hsu & Evans 1989).

Silvester & Hsu (1993) define that cove beaches can be in equilibrium in two ways: static equilibrium and dynamic equilibrium. In static equilibrium, the beach is in a stable situation, with zero longitudinal transport (assuming no sediment input or output from the bay). The dominant wave trains enter parallel to the coastline in the sheltered region and break simultaneously across the entire beach, resulting in almost no net littoral drift. However, if there is active sediment transport (sediment input or output), and the beach is in an unstable state, it can be considered in dynamic equilibrium. In this situation, littoral drift and sediment supply are determining factors in maintaining the beach width.

Morphological changes are usually caused by factors that modify the natural wave arrival trajectory on the beach, such as the presence of natural physical barriers like islands and rocky promontories, or man-made structures like jetties, breakwaters, and platforms (Short & Masselink, 1999).

Several analytical equations have been proposed to describe a form that best fits the coastline of cove beaches. Among these, notable equations include the Logarithmic Spiral equation (Yasso, 1965), the Parabolic equations (Hsu & Evans 1989), and the Hyperbolic equations (Moreno & Kraus, 1999). According to Klein et al. (2003), the model that best represents the planform shape of these beaches is Hsu & Evans (1989), as it not only provides a mathematical formulation defining the coastline from geometric data but also includes parameters related to the direction of the predominant wave and the point of wave diffraction, allowing for the measurement of the effects of changing these parameters.

When applying the parabolic equation manually, it becomes evident that this procedure is laborious and time-consuming due to the repetitive steps involved. Recognizing that the application of the equation could be expedited and facilitated with the aid of computational processing, the implementation of a system simulating the application of the parabolic equation for planform equilibrium of cove beaches was justified. This led to the development of the MEPBAY application, streamlining the learning process on this subject (Lausman et al., 2010).

 

REFERENCES:

• Hsu, J. R-C., Evans, C. Parabolic Bay Shapes and Applications. In: Institution of Civil Engineers – Part 2, 1989, Londres. Proceedings… Londres: Thomas Telford, 1989. p.557-570.
• Klein, A.H.F., Vargas, A., Raabe, A.L.A., Hsu, J.R.C. Visual assessment of bayedbeach stability with computer software. Computers & Geosciences 29, 1249–1257. 2003.
• Klein, A.H.F. Morphodynamics of Headland Bay Beaches. 450 p. Tese de Doutorado (Ciências do Mar) – Universidade do Algarve, Faro, Portugal. 2004.
• Moreno, L.J., Kraus, N.C. Equilibrium shape of headland-bay beaches for engineering design. In: Proceedings of Coastal Sediments ’99, Vol. 1. American Society of Civil Engineers, New York, pp. 860–875.
• Short, A. D., Masselink, G. Embayed and structurally controlled beaches. In: Short, A. D. (Ed.). Handbook of Beach and Shoreface Morphodynamics. New York: John Wiley & Sons, p.230-250. 1999.
• Silvester, R., Hsu, J.R.C. Coastal Stabilization. Advanced Series on Ocean Engineering. 14. Singapore: World Scientific, 578p. 1997.
• Silvester, R., Hsu, J.R.C. Coastal Stabilization: Innovative Concepts. Prentice-Hall, Englewood Cliffs, NJ. 578 pp. 1993.
• Vargas, A., Klein, A.H.F., Raabe, A.L.A., Modelo de Equilíbrio em Planta de Praia de Enseada, Itajaí. 2002.
• Yasso, W.E. Plan geometry of headland bay beaches. Journal of Geology 73, 702–714. 1965.
• Lausman, R., Klein, A.H.F., Stive, M., Uncertainty in the application of Parabolic Bay Shape Equation: A case study, Coastal Engineering, 2010.